| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Exercise 10.1 | Example 1 to 3 (Before Exercise 10.2) | Exercise 10.2 |
Chapter 10 Circles
Welcome to the solutions guide for Chapter 10, "Circles," from the latest Class 10 NCERT mathematics textbook for the academic session 2024-25. This chapter focuses specifically on the fascinating interaction between straight lines and circles, particularly exploring the properties and theorems related to tangents. Building upon previous knowledge about circles (chords, arcs, angles - covered in Class 9), this chapter introduces fundamental concepts and theorems governing tangents, which are essential for deeper understanding in geometry and related fields like coordinate geometry and calculus. These comprehensive solutions provide detailed explanations, rigorous proofs, and systematic applications for all the exercises presented.
The chapter begins by establishing clear definitions distinguishing different ways a line can interact with a circle. The solutions clarify the concepts of a secant (a line intersecting the circle at two distinct points) and, more importantly, a tangent (a line that touches the circle at exactly one point). This unique point is known as the point of contact. A key idea reinforced is that there can be only one tangent to a circle at any given point on its circumference. Building on this, the first fundamental theorem related to tangents is introduced, proved, and applied extensively in the solutions:
- Theorem 10.1: The tangent at any point of a circle is perpendicular to the radius through the point of contact.
The second cornerstone theorem explored in this chapter deals with tangents drawn from a point outside the circle. The solutions provide a rigorous proof for this theorem and demonstrate its wide-ranging applications:
- Theorem 10.2: The lengths of tangents drawn from an external point to a circle are equal.
The exercises covered by these solutions encompass a variety of problem types designed to solidify understanding and application skills. Students will find guidance on:
- Direct application of the two main theorems to calculate lengths or angles.
- Solving problems involving finding angles between tangents, radii, and chords connected to the point of contact.
- Proving geometric properties related to tangents, such as properties of quadrilaterals circumscribing a circle (e.g., proving opposite sides subtend supplementary angles at the centre).
Regarding the rationalized syllabus for 2024-25, Chapter 10, "Circles," has retained its core focus on the two fundamental theorems regarding tangents (tangent-radius perpendicularity and equal lengths of tangents from an external point) and their direct applications. The rationalization process primarily involved streamlining the number and complexity of exercises and proofs, ensuring students gain a solid mastery of these essential concepts without excessive intricacy. By diligently working through these comprehensive solutions, students can gain a thorough understanding of the properties of tangents, master the proofs of the key theorems, and develop confidence in applying these concepts to solve a variety of geometric problems involving circles.
Exercise 10.1
Question 1. How many tangents can a circle have?
Answer:
A circle can have infinitely many tangents.
Question 2. Fill in the blanks
(i) A tangent to a circle intersects it in_____________point (s).
(ii) A line intersecting a circle in two points is called a ____________________.
(iii) A circle can have __________________parallel tangents at the most.
(iv) The common point of a tangent to a circle and the circle is called _______________
Answer:
(i) A tangent to a circle intersects it in one point (s).
(ii) A line intersecting a circle in two points is called a secant.
(iii) A circle can have two parallel tangents at the most.
(iv) The common point of a tangent to a circle and the circle is called point of contact.
Question 3. A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is :
(A) 12 cm
(B) 13 cm
(C) 8.5 cm
(D) $\sqrt{119}$ cm.
Answer:
Given:
A circle with centre O and radius OP = 5 cm.
PQ is a tangent to the circle at point P.
A line from the centre O meets the tangent at Q, such that OQ = 12 cm.
To Find:
The length of the tangent segment PQ.
Solution:
We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Therefore, the radius OP is perpendicular to the tangent PQ at P.
$\angle OPQ = 90^\circ$
(Tangent is perpendicular to radius)
Consider the triangle $\triangle OPQ$. Since $\angle OPQ = 90^\circ$, it is a right-angled triangle.
By the Pythagorean theorem, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
In $\triangle OPQ$, OQ is the hypotenuse.
$(OQ)^2 = (OP)^2 + (PQ)^2$
(Pythagorean theorem)
Substitute the given values, OP = 5 cm and OQ = 12 cm:
$(12)^2 = (5)^2 + (PQ)^2$
... (i)
$144 = 25 + PQ^2$
Subtract 25 from both sides to find $PQ^2$:
$PQ^2 = 144 - 25$
$PQ^2 = 119$
Take the square root of both sides to find the length PQ:
$PQ = \sqrt{119}$ cm
... (ii)
The length of PQ is $\sqrt{119}$ cm.
Conclusion:
Comparing the result with the given options, the correct option is (D).
Question 4. Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
Answer:
Steps for Construction:
1. Draw a circle with any centre O and a suitable radius.
2. Draw a straight line $l$ outside, on, or intersecting the circle. This is the given line.
3. To draw a tangent parallel to line $l$: Draw a line perpendicular to $l$ passing through the centre O. This line will intersect the circle at two points. Draw a line through one of these intersection points that is perpendicular to the radius at that point. This new line will be a tangent to the circle and parallel to $l$. Let's call this line $m$.
4. To draw a secant parallel to line $l$: Draw another line perpendicular to $l$ passing through the interior of the circle. This line will intersect the circle at two points. Draw a line through these two intersection points. This new line will be a secant to the circle and parallel to $l$. Let's call this line $n$.
Description of the Figure:
The figure shows a circle with centre O.
A line $l$ is drawn somewhere in the plane.
A line $m$ is drawn such that $m || l$ and $m$ touches the circle at exactly one point (is a tangent).
A line $n$ is drawn such that $n || l$ and $n$ intersects the circle at two distinct points (is a secant).
There is a visual representation showing the circle, the original line, and the two lines parallel to it, one touching the circle and the other passing through it.
Example 1 to 3 (Before Exercise 10.2)
Example 1. Prove that in two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.
Answer:
Given:
Two concentric circles with common centre O.
A chord AB of the larger circle touches the smaller circle at point P.
To Prove:
The chord AB is bisected at the point of contact P, which means AP = PB.
Construction:
Join the centre O to the point of contact P. Join OA and OB (optional, but can help visualize the larger circle properties).
Proof:
We are given that AB is a tangent to the smaller circle at point P.
OP is the radius of the smaller circle to the point of contact P.
According to the theorem that states the tangent at any point of a circle is perpendicular to the radius through the point of contact, we have:
$OP \perp AB$
This implies that $\angle OPA = 90^\circ$ and $\angle OPB = 90^\circ$.
Now, consider the larger circle.
AB is a chord of the larger circle.
OP is a line segment from the centre O of the larger circle to the chord AB.
We have shown that $OP \perp AB$.
According to the theorem that states the perpendicular from the centre of a circle to a chord bisects the chord, the point P must be the midpoint of the chord AB.
Therefore, P bisects the chord AB.
This means that the length of segment AP is equal to the length of segment PB.
$AP = PB$
Hence, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.
This completes the proof.
Example 2. Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2 ∠OPQ.
Answer:
Given:
A circle with centre O.
TP and TQ are two tangents drawn from an external point T to the circle.
P and Q are the points of contact of the tangents.
To Prove:
$\angle PTQ = 2 \angle OPQ$
Proof:
We know that the tangents drawn from an external point to a circle are equal in length.
So, in the figure:
$TP = TQ$
(Tangents from external point T)
Consider the triangle $\triangle TPQ$. Since $TP = TQ$, $\triangle TPQ$ is an isosceles triangle.
In an isosceles triangle, the angles opposite the equal sides are equal.
Therefore,
$\angle TPQ = \angle TQP$
Let $\angle PTQ = \theta$.
The sum of angles in a triangle is $180^\circ$. In $\triangle TPQ$:
$\angle PTQ + \angle TPQ + \angle TQP = 180^\circ$
(Angle sum property of a triangle)
Substitute $\angle PTQ = \theta$ and $\angle TPQ = \angle TQP$:
$\theta + \angle TPQ + \angle TPQ = 180^\circ$
$\theta + 2 \angle TPQ = 180^\circ$
$2 \angle TPQ = 180^\circ - \theta$
$\angle TPQ = \frac{180^\circ - \theta}{2}$
$\angle TPQ = 90^\circ - \frac{\theta}{2}$
... (i)
We also know that the radius through the point of contact is perpendicular to the tangent.
So, the radius OP is perpendicular to the tangent TP at P.
$\angle OPT = 90^\circ$
(Radius $\perp$ Tangent at point of contact)
From the figure, $\angle OPT$ is the sum of $\angle OPQ$ and $\angle TPQ$:
$\angle OPT = \angle OPQ + \angle TPQ$
Substitute the value of $\angle OPT$ and the expression for $\angle TPQ$ from (i):
$90^\circ = \angle OPQ + (90^\circ - \frac{\theta}{2})$
Now, solve for $\angle OPQ$:
$90^\circ = \angle OPQ + 90^\circ - \frac{\theta}{2}$
$0 = \angle OPQ - \frac{\theta}{2}$
$\angle OPQ = \frac{\theta}{2}$
... (ii)
Since we defined $\theta = \angle PTQ$, we can substitute this back into equation (ii):
$\angle OPQ = \frac{1}{2} \angle PTQ$
Multiply both sides by 2:
$2 \angle OPQ = \angle PTQ$
Rearranging the terms, we get the desired result:
$\angle PTQ = 2 \angle OPQ$
Hence, proved.
Example 3. PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T (see Fig. 10.10). Find the length TP.
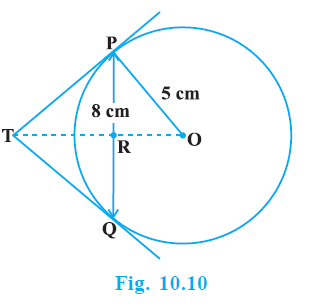
Answer:
Given:
A circle with centre O.
Chord PQ of length $8$ cm.
Radius of the circle $OP = OQ = 5$ cm.
Tangents at P and Q intersect at point T.
To Find:
The length of the tangent TP.
Solution:
We know that the tangents drawn from an external point to a circle are equal in length. Therefore, $TP = TQ$.
The line segment joining the centre to the external point T bisects the angle between the tangents ($\angle PTQ$) and also bisects the chord PQ perpendicularly.
So, the line segment TO bisects the chord PQ at point R, and $TO \perp PQ$.
This means R is the midpoint of PQ, and $\angle PRO = \angle TRO = 90^\circ$.
Length of PQ = $8$ cm.
$PR = RQ = \frac{1}{2} PQ$
(R is the midpoint of PQ)
$PR = RQ = \frac{1}{2} \times 8 \text{ cm} = 4 \text{ cm}$
Consider the right-angled triangle $\triangle ORP$. We have $OP = 5$ cm (radius) and $PR = 4$ cm.
By the Pythagorean theorem in $\triangle ORP$:
$OP^2 = OR^2 + PR^2$
$(5)^2 = OR^2 + (4)^2$
$25 = OR^2 + 16$
$OR^2 = 25 - 16$
$OR^2 = 9$
$OR = \sqrt{9} = 3$ cm
Now consider the triangles $\triangle RPT$ and $\triangle OPT$.
$\angle TRP = 90^\circ$ (Since $TO \perp PQ$)
$\angle OPT = 90^\circ$ (Radius is perpendicular to tangent at point of contact)
$\angle RTP = \angle OTP$ (Common angle to both triangles)
Therefore, by the AA similarity criterion, we have:
$\triangle RPT \sim \triangle OPT$
Since the triangles are similar, the ratio of their corresponding sides is equal:
$\frac{RP}{OP} = \frac{PT}{OT} = \frac{RT}{PT}$
From the ratio $\frac{RT}{PT} = \frac{RP}{OP}$:
$\frac{TR}{TP} = \frac{4}{5}$
This gives us $TR = \frac{4}{5} TP$.
From the ratio $\frac{PT}{OT} = \frac{RP}{OP}$:
$\frac{TP}{OT} = \frac{4}{5}$
This gives us $OT = \frac{5}{4} TP$.
From the figure, point R lies on the line segment OT. Therefore, $OT = OR + TR$.
Substitute the values we found for OT, OR, and TR:
$\frac{5}{4} TP = 3 + \frac{4}{5} TP$
Now, solve for TP:
$\frac{5}{4} TP - \frac{4}{5} TP = 3$
To subtract the terms with TP, find a common denominator, which is 20:
$\frac{5 \times 5}{4 \times 5} TP - \frac{4 \times 4}{5 \times 4} TP = 3$
$\frac{25}{20} TP - \frac{16}{20} TP = 3$
$\frac{25 TP - 16 TP}{20} = 3$
$\frac{9 TP}{20} = 3$
Multiply both sides by $\frac{20}{9}$ to isolate TP:
$TP = 3 \times \frac{20}{9}$
Simplify the expression by cancelling common factors:
$TP = \frac{\cancel{3}^{1} \times 20}{\cancel{9}_{3}}$
$TP = \frac{20}{3}$ cm
Final Answer:
The length of the tangent TP is $\frac{20}{3}$ cm.
Exercise 10.2
In Q.1 to 3, choose the correct option and give justification.
Question 1. From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
(A) 7 cm
(B) 12 cm
(C) 15 cm
(D) 24.5 cm
Answer:
Given:
Length of the tangent from point Q to the circle, PQ = 24 cm.
Distance of point Q from the centre O, OQ = 25 cm.
To Find:
The radius of the circle, OP.
Justification and Solution:
Let O be the centre of the circle and P be the point of contact of the tangent from Q to the circle.
We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Therefore, the radius OP is perpendicular to the tangent PQ at P.
$OP \perp PQ$
(Radius $\perp$ Tangent)
This means that the triangle $\triangle OPQ$ is a right-angled triangle with the right angle at P ($\angle OPQ = 90^\circ$).
We can use the Pythagorean theorem in the right-angled triangle $\triangle OPQ$. The hypotenuse is OQ (the side opposite the right angle).
$(OP)^2 + (PQ)^2 = (OQ)^2$
(Pythagorean theorem)
Substitute the given values, $PQ = 24$ and $OQ = 25$:
$(OP)^2 + (24)^2 = (25)^2$
... (i)
$OP^2 + 576 = 625$
Subtract 576 from both sides to find $OP^2$:
$OP^2 = 625 - 576$
$OP^2 = 49$
Take the square root of both sides to find OP:
$OP = \sqrt{49}$
$OP = 7$ cm
... (ii)
The radius of the circle is 7 cm.
Final Answer:
The correct option is (A) 7 cm.
Question 2. In Fig. 10.11, if TP and TQ are the two tangents to a circle with centre O so that ∠ POQ = 110°, then ∠ PTQ is equal to
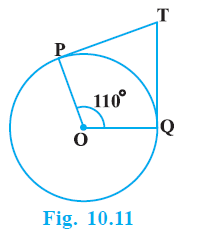
(A) 60°
(B) 70°
(C) 80°
(D) 90°
Answer:
Given:
TP and TQ are tangents to a circle with centre O.
$\angle POQ = 110^\circ$.
To Find:
The measure of $\angle PTQ$.
Justification and Solution:
We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Therefore, the radius OP is perpendicular to the tangent TP at P, and the radius OQ is perpendicular to the tangent TQ at Q.
$\angle OPT = 90^\circ$
(Radius $\perp$ Tangent)
$\angle OQT = 90^\circ$
(Radius $\perp$ Tangent)
Consider the quadrilateral OPTQ. The sum of the interior angles in a quadrilateral is $360^\circ$.
$\angle OPT + \angle PTQ + \angle TQO + \angle QOP = 360^\circ$
(Sum of angles in a quadrilateral)
Substitute the known values: $\angle OPT = 90^\circ$, $\angle TQO = 90^\circ$, and $\angle QOP = 110^\circ$:
$90^\circ + \angle PTQ + 90^\circ + 110^\circ = 360^\circ$
... (i)
Combine the constant terms:
$290^\circ + \angle PTQ = 360^\circ$
Subtract $290^\circ$ from both sides to solve for $\angle PTQ$:
$\angle PTQ = 360^\circ - 290^\circ$
$\angle PTQ = 70^\circ$
... (ii)
The measure of $\angle PTQ$ is $70^\circ$.
Final Answer:
The correct option is (B) $70^\circ$.
Question 3. If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then ∠POA is equal to
(A) 50°
(B) 60°
(C) 70°
(D) 80°
Answer:
Given:
PA and PB are tangents from external point P to a circle with centre O.
The angle between the tangents, $\angle APB = 80^\circ$.
To Find:
The measure of $\angle POA$.
Justification and Solution:
We know that the tangents drawn from an external point to a circle are equal in length.
$PA = PB$
(Tangents from external point P)
We also know that the line segment joining the centre to the external point bisects the angle between the tangents.
Thus, the line segment OP bisects $\angle APB$ and also bisects the angle subtended by the chord of contact at the centre ($\angle AOB$).
$\angle APO = \angle BPO$
(OP bisects $\angle APB$)
Since $\angle APB = 80^\circ$, we have:
$\angle APO = \angle BPO = \frac{1}{2} \angle APB = \frac{1}{2} \times 80^\circ = 40^\circ$
... (i)
We know that the radius through the point of contact is perpendicular to the tangent.
So, the radius OA is perpendicular to the tangent PA at A.
$\angle OAP = 90^\circ$
(Radius $\perp$ Tangent at point of contact)
Now, consider the right-angled triangle $\triangle OAP$.
The sum of angles in a triangle is $180^\circ$.
$\angle OAP + \angle APO + \angle POA = 180^\circ$
(Sum of angles in $\triangle OAP$)
Substitute the values $\angle OAP = 90^\circ$ and $\angle APO = 40^\circ$ (from (i)):
$90^\circ + 40^\circ + \angle POA = 180^\circ$
... (ii)
Combine the constant terms:
$130^\circ + \angle POA = 180^\circ$
Subtract $130^\circ$ from both sides to solve for $\angle POA$:
$\angle POA = 180^\circ - 130^\circ$
$\angle POA = 50^\circ$
... (iii)
Alternatively:
Consider $\triangle OAP$ and $\triangle OBP$.
$OA = OB$
(Radii of the same circle)
$PA = PB$
(Tangents from external point P)
$OP = OP$
(Common side)
Therefore, by SSS congruence rule:
$\triangle OAP \cong \triangle OBP$
By CPCT (Corresponding Parts of Congruent Triangles):
$\angle POA = \angle POB$
Also, $\angle OAP = \angle OBP = 90^\circ$ (Radius $\perp$ Tangent).
In quadrilateral OAPB, the sum of interior angles is $360^\circ$.
$\angle OAP + \angle APB + \angle PBO + \angle AOB = 360^\circ$
(Sum of angles in a quadrilateral)
Substitute the known values:
$90^\circ + 80^\circ + 90^\circ + \angle AOB = 360^\circ$
$260^\circ + \angle AOB = 360^\circ$
$\angle AOB = 360^\circ - 260^\circ = 100^\circ$
Since $\angle AOB = \angle POA + \angle POB$ and $\angle POA = \angle POB$, we have $\angle AOB = 2 \angle POA$.
$100^\circ = 2 \angle POA$
$\angle POA = \frac{100^\circ}{2} = 50^\circ$
Final Answer:
The measure of $\angle POA$ is $50^\circ$.
The correct option is (A) $50^\circ$.
Question 4. Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Answer:
Given:
A circle with centre O.
AB is a diameter of the circle.
Let line $l$ be the tangent to the circle at the end point A of the diameter.
Let line $m$ be the tangent to the circle at the other end point B of the diameter.
To Prove:
The tangents $l$ and $m$ are parallel, i.e., $l || m$.
Proof:
We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
The radius OA is drawn to the point of contact A of the tangent $l$.
Therefore, the radius OA is perpendicular to the tangent line $l$ at A.
$OA \perp l$
(Radius $\perp$ Tangent)
Since A, O, and B are collinear (as AB is a diameter), the diameter AB is perpendicular to the tangent $l$ at A.
Let's consider the angle formed by the tangent $l$ and the line AB. Let X be a point on line $l$ such that X and B are on opposite sides of A.
$\angle BAX = 90^\circ$
... (i)
Similarly, the radius OB is drawn to the point of contact B of the tangent $m$.
Therefore, the radius OB is perpendicular to the tangent line $m$ at B.
$OB \perp m$
(Radius $\perp$ Tangent)
Since A, O, and B are collinear, the diameter AB is perpendicular to the tangent $m$ at B.
Let Y be a point on line $m$ such that Y and A are on opposite sides of B.
$\angle ABY = 90^\circ$
... (ii)
Now, consider the lines $l$ and $m$ intersected by the transversal line AB.
The angles $\angle BAX$ (from equation (i)) and $\angle ABY$ (from equation (ii)) are alternate interior angles formed by the transversal AB with lines $l$ and $m$.
From equations (i) and (ii), we have $\angle BAX = 90^\circ$ and $\angle ABY = 90^\circ$.
$\angle BAX = \angle ABY$
= $90^\circ$
... (iii)
Since the alternate interior angles formed by the transversal AB are equal, the lines $l$ and $m$ must be parallel.
$l || m$
Therefore, the tangents drawn at the ends of a diameter of a circle are parallel.
This completes the proof.
Question 5. Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Answer:
Given:
A circle with centre O.
A tangent line $l$ touches the circle at point P.
To Prove:
The line perpendicular to the tangent $l$ at the point of contact P passes through the centre O.
Proof:
Let the tangent to the circle at point P be the line $l$.
OP is the radius of the circle joining the centre O to the point of contact P.
We know from a theorem that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Therefore, the radius OP is perpendicular to the tangent line $l$ at the point of contact P.
$OP \perp l$
(Radius $\perp$ Tangent)
Now, consider the line OP. This line passes through the centre O and is perpendicular to the tangent $l$ at P.
From basic geometry, we know that through a given point on a given line, there exists one and only one line perpendicular to the given line.
In our case, the given line is the tangent $l$, and the given point on the line is the point of contact P.
The line OP is one line that is perpendicular to $l$ at P.
According to the uniqueness principle mentioned above, any other line that is perpendicular to the tangent $l$ at the point P must coincide with the line OP.
Since the line OP passes through the centre O (by its construction as a radius connecting the centre to a point on the circle), it logically follows that the perpendicular line to the tangent at the point of contact P must pass through the centre O.
This completes the proof.
Question 6. The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Answer:
Given:
A point A is at a distance of 5 cm from the centre O of the circle. OA = 5 cm.
Let P be the point of contact of the tangent from A to the circle.
The length of the tangent from A to the circle, AP = 4 cm.
To Find:
The radius of the circle, OP.
Solution:
Let O be the centre of the circle and P be the point of contact of the tangent from point A to the circle.
We are given OA = 5 cm and AP = 4 cm. OP is the radius we need to find.
We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Therefore, the radius OP is perpendicular to the tangent AP at the point of contact P.
$OP \perp AP$
(Radius $\perp$ Tangent)
This means that $\triangle OPA$ is a right-angled triangle with the right angle at P ($\angle OPA = 90^\circ$).
According to the Pythagorean theorem, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
In $\triangle OPA$, the hypotenuse is OA (the side opposite the right angle).
So, by the Pythagorean theorem:
$(OP)^2 + (AP)^2 = (OA)^2$
(Pythagorean theorem)
Substitute the given values, $AP = 4$ and $OA = 5$:
$(OP)^2 + (4)^2 = (5)^2$
... (i)
Calculate the squares:
$OP^2 + 16 = 25$
Subtract 16 from both sides to solve for $OP^2$:
$OP^2 = 25 - 16$
$OP^2 = 9$
Take the square root of both sides to find the radius OP:
$OP = \sqrt{9}$
$OP = 3$ cm
... (ii)
The radius of the circle is 3 cm.
Final Answer:
The radius of the circle is 3 cm.
Question 7. Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Answer:
Given:
Two concentric circles with common centre O.
Radius of the smaller circle, $r = 3$ cm.
Radius of the larger circle, $R = 5$ cm.
A chord AB of the larger circle touches the smaller circle at point P.
To Find:
The length of the chord AB.
Solution:
Let O be the centre of the two concentric circles.
The radius of the smaller circle is $OP = r = 3$ cm, where P is the point of contact of the chord AB with the smaller circle.
The radius of the larger circle is $OA = OB = R = 5$ cm.
We know that the tangent to a circle is perpendicular to the radius through the point of contact.
Since AB is a tangent to the smaller circle at P, the radius OP is perpendicular to the chord AB.
$OP \perp AB$
(Radius $\perp$ Tangent)
This means that the angle $\angle OPA = 90^\circ$.
Consider the triangle $\triangle OPA$. It is a right-angled triangle at P.
According to the Pythagorean theorem, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
In $\triangle OPA$, OA is the hypotenuse.
$(OP)^2 + (AP)^2 = (OA)^2$
(Pythagorean theorem)
Substitute the known values, $OP = 3$ and $OA = 5$:
$(3)^2 + (AP)^2 = (5)^2$
... (i)
Calculate the squares:
$9 + AP^2 = 25$
Subtract 9 from both sides to solve for $AP^2$:
$AP^2 = 25 - 9$
$AP^2 = 16$
Take the square root of both sides to find the length AP:
$AP = \sqrt{16}$
$AP = 4$ cm
... (ii)
Now, consider the larger circle. AB is a chord of the larger circle, and OP is a line segment from the centre O perpendicular to the chord AB at P.
According to the theorem which states that the perpendicular from the centre of a circle to a chord bisects the chord, the point P is the midpoint of the chord AB.
$AP = PB$
(Perpendicular from centre bisects chord)
The total length of the chord AB is the sum of the lengths AP and PB:
$AB = AP + PB$
Since $AP = PB$, we have:
$AB = 2 \times AP$
Substitute the value of AP from equation (ii):
$AB = 2 \times 4$
$AB = 8$ cm
... (iii)
The length of the chord of the larger circle which touches the smaller circle is 8 cm.
Final Answer:
The length of the chord is 8 cm.
Question 8. A quadrilateral ABCD is drawn to circumscribe a circle (see Fig. 10.12). Prove that AB + CD = AD + BC
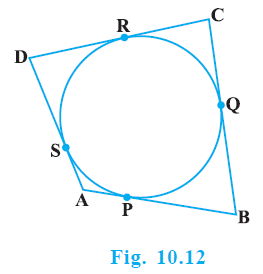
Answer:
Given:
A quadrilateral ABCD is drawn to circumscribe a circle with centre O.
The sides AB, BC, CD, and DA touch the circle at points P, Q, R, and S respectively.
To Prove:
$AB + CD = AD + BC$
Proof:
We know that the lengths of tangents drawn from an external point to a circle are equal.
Considering the vertices of the quadrilateral as external points, we have:
From point A, the tangents are AP and AS.
$AP = AS$
... (1)
From point B, the tangents are BP and BQ.
$BP = BQ$
... (2)
From point C, the tangents are CR and CQ.
$CR = CQ$
... (3)
From point D, the tangents are DR and DS.
$DR = DS$
... (4)
Add equations (1), (2), (3), and (4):
$(AP + BP) + (CR + DR) = (AS + BQ) + (CQ + DS)$
Rearrange the terms on the Right Hand Side (RHS):
$(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)$
From the figure, we can see that the sides of the quadrilateral are formed by the sum of these tangent segments:
$AB = AP + PB$ (or $AP + BP$)
$CD = CR + RD$ (or $CR + DR$)
$AD = AS + SD$ (or $AS + DS$)
$BC = BQ + QC$ (or $BQ + CQ$)
Substitute these expressions for the sides back into the equation we obtained by adding the tangent lengths:
$AB + CD = AD + BC$
Thus, the sum of the pairs of opposite sides of the quadrilateral circumscribing a circle are equal.
Hence, proved.
Question 9. In Fig. 10.13, XY and X′Y′ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X′Y′ at B. Prove that ∠ AOB = 90°.
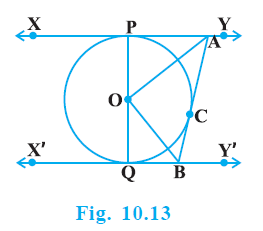
Answer:
Given:
A circle with centre O.
XY and X′Y′ are two parallel tangents to the circle, with points of contact P and Q respectively.
AB is another tangent to the circle at point C, intersecting XY at A and X′Y′ at B.
To Prove:
$\angle AOB = 90^\circ$
Construction:
Join the centre O to the points of contact P, Q, and C. Also, join OA and OB.
Proof:
Since XY and X′Y′ are parallel tangents, the line segment PQ joining their points of contact must pass through the centre O and is a diameter of the circle.
Therefore, POQ is a straight line.
$\angle POQ = 180^\circ$
(Angles on a straight line)
Consider the tangents from point A to the circle, which are AP and AC.
We know that the lengths of tangents drawn from an external point to a circle are equal.
$AP = AC$
(Tangents from A)
Now, consider $\triangle OAP$ and $\triangle OCA$.
$OP = OC$
(Radii of the same circle)
$OA = OA$
(Common side)
$AP = AC$
(Proved above)
Therefore, by SSS congruence rule, $\triangle OAP$ is congruent to $\triangle OCA$.
$\triangle OAP \cong \triangle OCA$
By CPCT (Corresponding Parts of Congruent Triangles), the corresponding angles are equal:
$\angle POA = \angle COA$
... (1)
Similarly, consider the tangents from point B to the circle, which are BQ and BC.
$BQ = BC$
(Tangents from B)
Now, consider $\triangle OQB$ and $\triangle OCB$.
$OQ = OC$
(Radii of the same circle)
$OB = OB$
(Common side)
$BQ = BC$
(Proved above)
Therefore, by SSS congruence rule, $\triangle OQB$ is congruent to $\triangle OCB$.
$\triangle OQB \cong \triangle OCB$
By CPCT, the corresponding angles are equal:
$\angle QOB = \angle COB$
... (2)
Since POQ is a straight line, the sum of the angles around O on this line is $180^\circ$.
$\angle POQ = \angle POA + \angle COA + \angle COB + \angle QOB$
$\angle POA + \angle COA + \angle COB + \angle QOB = 180^\circ$
Substitute the equal angles from equations (1) and (2) into this equation:
$\angle COA + \angle COA + \angle COB + \angle COB = 180^\circ$
$2 \angle COA + 2 \angle COB = 180^\circ$
Factor out 2 from the left side:
$2 (\angle COA + \angle COB) = 180^\circ$
Divide both sides by 2:
$\angle COA + \angle COB = \frac{180^\circ}{2}$
$\angle COA + \angle COB = 90^\circ$
... (3)
From the figure, the angle $\angle AOB$ is the sum of angles $\angle COA$ and $\angle COB$:
$\angle AOB = \angle COA + \angle COB$
Substitute the result from equation (3) into this:
$\angle AOB = 90^\circ$
Hence, proved that $\angle AOB = 90^\circ$.
Question 10. Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
Answer:
Given:
A circle with centre O.
P is an external point.
PA and PB are two tangents drawn from P to the circle, touching the circle at points A and B respectively.
To Prove:
The angle between the tangents ($\angle APB$) and the angle subtended by the line-segment joining the points of contact at the centre ($\angle AOB$) are supplementary.
That is, $\angle APB + \angle AOB = 180^\circ$.
Proof:
Let O be the centre of the circle, and P be the external point from which two tangents PA and PB are drawn to the circle, touching it at points A and B respectively.
We know that the radius through the point of contact is perpendicular to the tangent at that point.
Therefore, the radius OA is perpendicular to the tangent PA at the point of contact A.
$OA \perp PA$
This implies that the angle $\angle OAP$ is a right angle.
$\angle OAP = 90^\circ$
(Radius $\perp$ Tangent)
Similarly, the radius OB is perpendicular to the tangent PB at the point of contact B.
$OB \perp PB$
This implies that the angle $\angle OBP$ is a right angle.
$\angle OBP = 90^\circ$
(Radius $\perp$ Tangent)
Now, consider the quadrilateral OAPB. The sum of the interior angles of a quadrilateral is $360^\circ$.
The angles of quadrilateral OAPB are $\angle OAP$, $\angle APB$, $\angle PBO$ (or $\angle OBP$), and $\angle BOA$ (or $\angle AOB$).
So, the sum of these angles is:
$\angle OAP + \angle APB + \angle OBP + \angle AOB = 360^\circ$
(Sum of angles in quadrilateral OAPB)
Substitute the known values for $\angle OAP$ and $\angle OBP$ ($90^\circ$ each) into the equation:
$90^\circ + \angle APB + 90^\circ + \angle AOB = 360^\circ$
Combine the constant terms:
$180^\circ + \angle APB + \angle AOB = 360^\circ$
Subtract $180^\circ$ from both sides of the equation:
$\angle APB + \angle AOB = 360^\circ - 180^\circ$
$\angle APB + \angle AOB = 180^\circ$
Since the sum of the two angles $\angle APB$ and $\angle AOB$ is $180^\circ$, they are supplementary angles.
Thus, the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
Hence, proved.
Question 11. Prove that the parallelogram circumscribing a circle is a rhombus.
Answer:
Given:
A parallelogram ABCD is drawn to circumscribe a circle.
Let the sides AB, BC, CD, and DA touch the circle at points P, Q, R, and S respectively.
To Prove:
ABCD is a rhombus.
Proof:
Since ABCD is a parallelogram circumscribing a circle, its sides are tangent to the circle.
We know that the lengths of tangents drawn from an external point to a circle are equal.
Considering the vertices of the parallelogram as external points, we have:
From point A, the tangents are AP and AS.
$AP = AS$
... (1)
From point B, the tangents are BP and BQ.
$BP = BQ$
... (2)
From point C, the tangents are CR and CQ.
$CR = CQ$
... (3)
From point D, the tangents are DR and DS.
$DR = DS$
... (4)
The sides of the parallelogram can be expressed as the sum of these tangent segments:
$AB = AP + PB$
... (5)
$BC = BQ + QC$
... (6)
$CD = CR + RD$
... (7)
$DA = DS + SA$
... (8)
Add the lengths of the sides AB and CD:
$AB + CD = (AP + BP) + (CR + DR)$
Add the lengths of the sides AD and BC:
$AD + BC = (AS + DS) + (BQ + CQ)$
Substitute the equal tangent lengths from equations (1) to (4) into the sum of AD and BC:
$AD + BC = (AP + DR) + (BP + CR)$
Rearrange the terms:
$AD + BC = (AP + BP) + (DR + CR)$
From equations (5) and (7), we see this is equal to $AB + CD$.
$AD + BC = AB + CD$
... (9)
This shows that the sum of opposite sides is equal.
Since ABCD is a parallelogram, we know that opposite sides are equal:
$AB = CD$
... (10)
$BC = DA$ (or $AD$)
... (11)
Substitute (10) and (11) into equation (9):
$AD + AD = AB + AB$
$2 AD = 2 AB$
$AD = AB$
... (12)
From (10), (11), and (12), we have:
$AB = CD$
$AD = BC$
$AB = AD$
Combining these, we get:
$AB = BC = CD = DA$
Since ABCD is a parallelogram and all its sides are equal in length, it is a rhombus.
Hence, proved.
Question 12. A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see Fig. 10.14). Find the sides AB and AC.
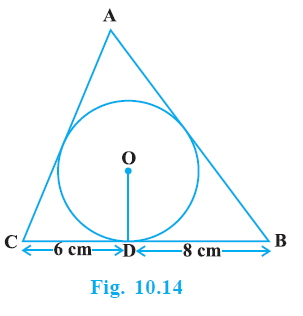
Answer:
Given:
A triangle ABC circumscribes a circle with centre O and radius $r = 4$ cm.
The point of contact on BC is D, dividing BC into segments BD and DC.
$BD = 8$ cm.
$DC = 6$ cm.
To Find:
The lengths of the sides AB and AC.
Solution:
Let the circle touch the sides AB and AC at points E and F respectively.
We know that the lengths of tangents drawn from an external point to a circle are equal.
From external point B, tangents are BD and BE.
$BE = BD$
(Tangents from B)
$BE = 8$ cm
From external point C, tangents are CD and CF.
$CF = CD$
(Tangents from C)
$CF = 6$ cm
From external point A, tangents are AE and AF.
$AE = AF$
(Tangents from A)
Let $AE = AF = x$ cm.
Now, we can write the lengths of the sides of the triangle ABC:
$AB = AE + EB = x + 8$ cm
$AC = AF + FC = x + 6$ cm
$BC = BD + DC = 8 + 6 = 14$ cm
The radius of the inscribed circle is $r = OD = OE = OF = 4$ cm.
We know that the radius is perpendicular to the tangent at the point of contact. So, $OD \perp BC$, $OE \perp AB$, and $OF \perp AC$.
The area of $\triangle ABC$ can be calculated in two ways:
Method 1: Using the sum of areas of $\triangle OBC$, $\triangle OCA$, and $\triangle OAB$.
Join the vertices A, B, C to the centre O. Also, join O to the points of contact D, E, F.
The height of each of the triangles $\triangle OBC$, $\triangle OCA$, and $\triangle OAB$ from the base (side of $\triangle ABC$) to the centre O is the radius of the inscribed circle (4 cm).
Area($\triangle OBC$) = $\frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times BC \times OD$
Area($\triangle OBC$) = $\frac{1}{2} \times 14 \times 4 = 7 \times 4 = 28$ cm$^2$
Area($\triangle OCA$) = $\frac{1}{2} \times AC \times OF = \frac{1}{2} \times (x+6) \times 4$
Area($\triangle OCA$) = $2(x+6) = (2x+12)$ cm$^2$
Area($\triangle OAB$) = $\frac{1}{2} \times AB \times OE = \frac{1}{2} \times (x+8) \times 4$
Area($\triangle OAB$) = $2(x+8) = (2x+16)$ cm$^2$
Total Area($\triangle ABC$) = Area($\triangle OBC$) + Area($\triangle OCA$) + Area($\triangle OAB$)
Area($\triangle ABC$) = $28 + (2x+12) + (2x+16)$
Area($\triangle ABC$) = $4x + 56$ cm$^2$
... (1)
Method 2: Using Heron's Formula.
The sides of $\triangle ABC$ are $a = BC = 14$, $b = AC = x+6$, $c = AB = x+8$.
The semi-perimeter $s$ of $\triangle ABC$ is:
$s = \frac{AB + BC + AC}{2} = \frac{(x+8) + 14 + (x+6)}{2}$
$s = \frac{2x + 28}{2} = x + 14$
Now calculate $s-a$, $s-b$, and $s-c$:
$s-a = (x+14) - 14 = x$
$s-b = (x+14) - (x+6) = 8$
$s-c = (x+14) - (x+8) = 6$
According to Heron's formula, the Area($\triangle ABC$) is:
Area($\triangle ABC$) = $\sqrt{s(s-a)(s-b)(s-c)}$
Area($\triangle ABC$) = $\sqrt{(x+14)(x)(8)(6)}$
Area($\triangle ABC$) = $\sqrt{48x(x+14)}$ cm$^2$
... (2)
Equate the two expressions for the Area($\triangle ABC$) from (1) and (2):
$4x + 56 = \sqrt{48x(x+14)}$
Factor out 4 from the left side:
$4(x + 14) = \sqrt{48x(x+14)}$
Square both sides of the equation:
$(4(x + 14))^2 = (\sqrt{48x(x+14)})^2$
$16(x + 14)^2 = 48x(x+14)$
$16(x + 14)(x + 14) = 48x(x+14)$
Since x represents a length, $x \geq 0$. For a valid triangle, $x+14 > 0$. So we can divide both sides by $16(x+14)$:
$\frac{\cancel{16}\cancel{(x + 14)}(x + 14)}{\cancel{16}\cancel{(x + 14)}} = \frac{\cancel{48}^{3}x\cancel{(x+14)}}{\cancel{16}\cancel{(x + 14)}}$
$x + 14 = 3x$
Subtract $x$ from both sides:
$14 = 3x - x$
$14 = 2x$
Divide both sides by 2:
$x = \frac{14}{2}$
$x = 7$
Now we can find the lengths of sides AB and AC:
$AB = x + 8 = 7 + 8 = 15$ cm
$AC = x + 6 = 7 + 6 = 13$ cm
Final Answer:
The lengths of the sides AB and AC are $15$ cm and $13$ cm respectively.
Question 13. Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Answer:
Let the quadrilateral be ABCD, circumscribing a circle with centre O. Let the sides AB, BC, CD, and DA touch the circle at points P, Q, R, and S respectively.
Given:
ABCD is a quadrilateral circumscribing a circle with centre O. The sides AB, BC, CD, DA touch the circle at P, Q, R, S respectively.
To Prove:
Opposite sides subtend supplementary angles at the centre O. That is, $\angle AOB + \angle COD = 180^\circ$ and $\angle BOC + \angle DOA = 180^\circ$.
Construction Required:
Join OA, OB, OC, OD. Also join OP, OQ, OR, OS.
Proof:
Consider the triangles $\triangle APO$ and $\triangle ASO$.
We have:
OP = OS
(Radii of the same circle)
OA = OA
(Common side)
AP = AS
(Lengths of tangents from an external point A are equal)
Therefore, $\triangle APO \cong \triangle ASO$ by the SSS congruence rule.
$\triangle APO \cong \triangle ASO$
(SSS Congruence Rule)
By Corresponding Parts of Congruent Triangles (CPCT), we have:
$\angle AOP = \angle AOS$
(CPCT)
Let $\angle AOP = \angle AOS = x^\circ$.
Similarly, considering the pairs of triangles formed by the centre O and the points of contact from vertices B, C, and D, we can prove their congruence:
$\triangle BPO \cong \triangle BQO$
$\triangle BPO \cong \triangle BQO$
(SSS Congruence Rule)
This implies:
$\angle BOP = \angle BOQ$
(CPCT)
Let $\angle BOP = \angle BOQ = y^\circ$.
$\triangle CQO \cong \triangle CRO$
$\triangle CQO \cong \triangle CRO$
(SSS Congruence Rule)
This implies:
$\angle COQ = \angle COR$
(CPCT)
Let $\angle COQ = \angle COR = z^\circ$.
$\triangle DRO \cong \triangle DSO$
$\triangle DRO \cong \triangle DSO$
(SSS Congruence Rule)
This implies:
$\angle DOR = \angle DOS$
(CPCT)
Let $\angle DOR = \angle DOS = w^\circ$.
The sum of all angles around the centre O is $360^\circ$.
So, $\angle AOP + \angle AOS + \angle BOP + \angle BOQ + \angle COQ + \angle COR + \angle DOR + \angle DOS = 360^\circ$.
Substitute the angles in terms of $x, y, z, w$:
$x + x + y + y + z + z + w + w = 360^\circ$
$2x + 2y + 2z + 2w = 360^\circ$
Factor out 2:
$2(x + y + z + w) = 360^\circ$
Divide by 2:
$x + y + z + w = 180^\circ$
... (i)
Now, consider the angles subtended by the opposite sides AB and CD at the centre:
$\angle AOB = \angle AOP + \angle BOP = x + y$
$\angle COD = \angle COQ + \angle DOR = z + w$
The sum of these angles is:
$\angle AOB + \angle COD = (x + y) + (z + w) = x + y + z + w$
From equation (i), we know that $x + y + z + w = 180^\circ$.
Therefore,
$\angle AOB + \angle COD = 180^\circ$
Thus, the angles subtended by opposite sides AB and CD at the centre are supplementary.
Similarly, consider the angles subtended by the opposite sides BC and DA at the centre:
$\angle BOC = \angle BOQ + \angle COQ = y + z$
$\angle DOA = \angle DOS + \angle AOS = w + x$
The sum of these angles is:
$\angle BOC + \angle DOA = (y + z) + (w + x) = x + y + z + w$
From equation (i), we know that $x + y + z + w = 180^\circ$.
Therefore,
$\angle BOC + \angle DOA = 180^\circ$
Thus, the angles subtended by opposite sides BC and DA at the centre are supplementary.
Hence, proved.

